
Le cône de Lot et ses filles se développe sous la forme extraordinairement simple d'un parallélogramme parfait. A l'occasion de sa fabrication, Hubert Le Menestrel a fait une intéressante découverte mathématique, qui lui a permis d'établir le théorème suivant :
Théorème :
Lorsqu'on forme un cône par pliage d'une surface plane, en superposant deux demi-droites opposées, l'angle au sommet du cône vaut 60 degrés.
Démonstration :
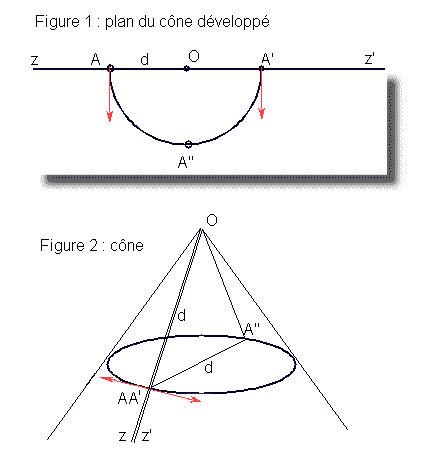
La figure 1 montre le plan du cône développé : il va être formé par déformation de ce plan, venant superposer les demi-droites Oz et Oz'. Le point A' va venir se superposer au point A.
Le demi-cercle AA"A' va devenir, dans le cône, un cercle perpendiculaire à l'axe du cône comme montré Figure 2. Les tangentes au demi-cercle, dans le plan, qui sont perpendiculaires à zz', vont se confondre comme tangentes au cône.
Si d est la distance OA, le demi-cercle a pour longueur (pi x d) ; c'est aussi la longueur de la circonférence dans le cône, et le diamètre de cette circonférence est donc d. Le triangle OAA" (A" étant le point opposé à A sur le cercle) est donc équilatéral. L'angle au sommet du cône est donc 60°.
CQFD.